[转]拜托，面试别再问我时间复杂度了

最烦面试官问，“为什么XX算法的时间复杂度是OO”，今后，不再惧怕这类问题。

快速排序分为这么几步：

第一步，先做一次partition；

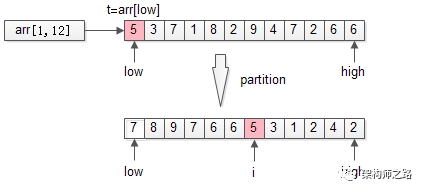
partition使用第一个元素t=arr[low]为哨兵，把数组分成了两个半区：

• 左半区比t大
• 右半区比t小

第二步，左半区递归；

第三步，右半区递归；

 

伪代码为：

void quick_sort(int[]arr, int low, int high){

if(low== high) return;

int i = partition(arr, low, high);

quick_sort(arr, low, i-1);

quick_sort(arr, i+1, high);

}

为啥，快速排序，时间复杂度是O(n*lg(n))呢？

今天和大家聊聊时间复杂度。

画外音：往下看，第三类方法很牛逼。

第一大类，简单规则

为方便记忆，先总结几条简单规则，热热身。

 

规则一：“有限次操作”的时间复杂度往往是O(1)。

例子：交换两个数a和b的值。

void swap(int& a, int& b){

int t=a;

a=b;

b=t;

}

 

分析：通过了一个中间变量t，进行了3次操作，交换了a和b的值，swap的时间复杂度是O(1)。

画外音：这里的有限次操作，是指不随数据量的增加，操作次数增加。

 

规则二：“for循环”的时间复杂度往往是O(n)。

例子：n个数中找到最大值。

int max(int[] arr, int n){

int temp = -MAX;

for(int i=0;i<n;++i)

if(arr[i]>temp) temp=arr[i];

return temp;

}

 

分析：通过一个for循环，将数据集遍历，每次遍历，都只执行“有限次操作”，计算的总次数，和输入数据量n呈线性关系。

 

规则三：“树的高度”的时间复杂度往往是O(lg(n))。

分析：树的总节点个数是n，则树的高度是lg(n)。

 

在一棵包含n个元素二分查找树上进行二分查找，其时间复杂度是O(lg(n))。

对一个包含n个元素的堆顶元素弹出后，调整成一个新的堆，其时间复杂度也是O(lg(n))。

 

第二大类：组合规则

通过简单规则的时间复杂度，来求解组合规则的时间复杂度。

 

例如：n个数冒泡排序。

void bubble_sort(int[] arr, int n){

for(int i=0;i<n;i++)

for(int j=0;j<n-i-1;j++)

if(arr[j]>arr[j+1])

swap(arr[j], arr[j+1]);

}

 

分析：冒泡排序，可以看成三个规则的组合：

1. 外层for循环

2. 内层for循环

3. 最内层的swap

 

故，冒泡排序的时间复杂度为：

O(n) * O(n) * O(1) = O(n^2)

 

又例如：TopK问题，通过建立k元素的堆，来从n个数中求解最大的k个数。

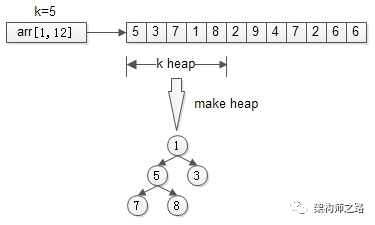
先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。

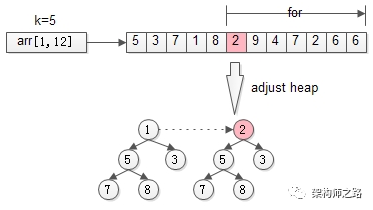
接着，从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。

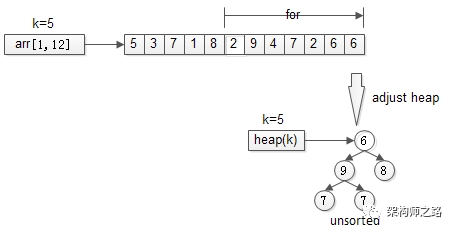
直到，扫描完所有n-k个元素，最终堆中的k个元素，就是为所求的TopK。

 

伪代码：

heap[k] = make_heap(arr[1, k]);

for(i=k+1 to n){

adjust_heap(heep[k],arr[i]);

}

return heap[k];

 

分析：可以看成三个规则的组合：

1. 新建堆

2. for循环

3. 调整堆

 

故，用堆求解TopK，时间复杂度为：

O(k) + O(n) * O(lg(k)) = O(n*lg(k))

画外音：注意哪些地方用加，哪些地方用乘；哪些地方是n，哪些地方是k。

 

第三大类，递归求解

简单规则和组合规则可以用来求解非递归的算法的时间复杂度。对于递归的算法，该怎么分析呢？

 

接下来，通过几个案例，来说明如何通分析递归式，来分析递归算法的时间复杂度。

 

案例一：计算 1到n的和，时间复杂度分析。

 

如果用非递归的算法：

int sum(int n){

int result=0;

for(int i=0;i<n;i++)

result += i;

return result;

}

根据简单规则，for循环，sum的时间复杂度是O(n)。

 

但如果是递归算法，就没有这么直观了：

int sum(int n){

if (n==1) return 1;

return n+sum(n-1);

}

 

如何来进行时间复杂度分析呢？

 

用f(n)来表示数据量为n时，算法的计算次数，很容易知道：

• 当n=1时，sum函数只计算1次

画外音：if (n==1) return 1;

即：

f(1)=1【式子A】

 

不难发现，当n不等于1时：

• f(n)的计算次数，等于f(n-1)的计算次数，再加1次计算

画外音：return n+sum(n-1);

即：

f(n)=f(n-1)+1【式子B】

 

【式子B】不断的展开，再配合【式子A】：

画外音：这一句话，是分析这个算法的关键。

f(n)=f(n-1)+1

f(n-1)=f(n-2)+1

…

f(2)=f(1)+1

f(1)=1

 

上面共n个等式，左侧和右侧分别相加：

f(n)+f(n-1)+…+f(2)+f(1)

=

[f(n-1)+1]+[f(n-2)+1]+…+[f(1)+1]+[1]

 

即得到：

f(n)=n

已经有那么点意思了哈，再来个复杂点的算法。

案例二：二分查找binary_search，时间复杂度分析。

int BS(int[] arr, int low, int high, int target){

if (low>high) return -1;

mid = (low+high)/2;

if (arr[mid]== target) return mid;

if (arr[mid]> target)

return BS(arr, low, mid-1, target);

else

return BS(arr, mid+1, high, target);

}

 

二分查找，单纯从递归算法来分析，怎能知道其时间复杂度是O(lg(n))呢？

 

仍用f(n)来表示数据量为n时，算法的计算次数，很容易知道：

• 当n=1时，bs函数只计算1次

画外音：不用纠结是1次还是1.5次，还是2.7次，是一个常数次。

即：

f(1)=1【式子A】

 

在n很大时，二分会进行一次比较，然后进行左侧或者右侧的递归，以减少一半的数据量：

• f(n)的计算次数，等于f(n/2)的计算次数，再加1次计算

画外音：计算arr[mid]>target，再减少一半数据量迭代

即：

f(n)=f(n/2)+1【式子B】

【式子B】不断的展开，

f(n)=f(n/2)+1

f(n/2)=f(n/4)+1

f(n/4)=f(n/8)+1

…

f(n/2^(m-1))=f(n/2^m)+1

 

上面共m个等式，左侧和右侧分别相加：

f(n)+f(n/2)+…+f(n/2^(m-1))

=

[f(n/2)+1]+[f(n/4)+1]+…+[f(n/2^m)]+[1]

即得到：

f(n)=f(n/2^m)+m

 

再配合【式子A】：

f(1)=1

即，n/2^m=1时, f(n/2^m)=1, 此时m=lg(n), 这一步，这是分析这个算法的关键。

 

将m=lg(n)带入，得到：

f(n)=1+lg(n)

 

神奇不神奇？

 

最后，大boss，快速排序递归算法，时间复杂度的分析过程。

 

案例三：快速排序quick_sort，时间复杂度分析。

void quick_sort(int[]arr, int low, int high){

if (low==high) return;

int i = partition(arr, low, high);

quick_sort(arr, low, i-1);

quick_sort(arr, i+1, high);

}

 

仍用f(n)来表示数据量为n时，算法的计算次数，很容易知道：

• 当n=1时，quick_sort函数只计算1次

f(1)=1【式子A】

 

在n很大时：

第一步，先做一次partition；

第二步，左半区递归；

第三步，右半区递归；

即：

f(n)=n+f(n/2)+f(n/2)=n+2*f(n/2)【式子B】

画外音：

(1)partition本质是一个for，计算次数是n；

(2)二分查找只需要递归一个半区，而快速排序左半区和右半区都要递归，这一点在分治法与减治法一章节已经详细讲述过；

 

【式子B】不断的展开，

f(n)=n+2*f(n/2)

f(n/2)=n/2+2*f(n/4)

f(n/4)=n/4+2*f(n/8)

…

f(n/2^(m-1))=n/2^(m-1)+2f(n/2^m)

 

上面共m个等式，逐步带入，于是得到：

f(n)=n+2*f(n/2)

=n+2*[n/2+2*f(n/4)]=2n+4*f(n/4)

=2n+4*[n/4+2*f(n/8)]=3n+8f(n/8)

=…

=m*n+2^m*f(n/2^m)

 

再配合【式子A】：

f(1)=1

即，n/2^m=1时, f(n/2^m)=1, 此时m=lg(n), 这一步，这是分析这个算法的关键。

将m=lg(n)带入，得到：

f(n)=lg(n)*n+2^(lg(n))*f(1)=n*lg(n)+n

 

故，快速排序的时间复杂度是n*lg(n)。

 

[resouce]拜托，面试别再问我时间复杂度了